

Sie befinden sich hier: Home : Industriegase Lexikon: Viskosität
Bewegt sich ein fester Körpers durch ein Fluid (Gas oder Flüssigkeit) oder strömt ein Fluid durch
einen Kanal, muss eine Kraft aufgebracht werden, um den Reibungswiderstand zu überwinden.
Die Viskosität der Fluide ist ein Maß für den geleisteten Widerstand gegen eine Formänderung.
Die Viskosität oder auch Zähigkeit kann wie folgt erklärt werden:
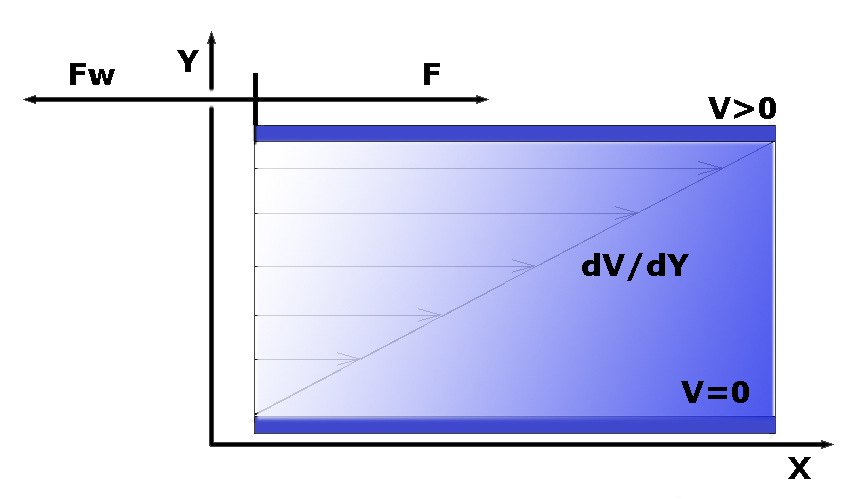
Man Betrachtet zwei parallele Platten mit der Fläche "A" und dem Abstand "Y" zwischen denen sich ein Fluid befindet das an beiden Platten haftet.
Wird eine der beiden Platten mit der Geschwindigkeit "V" bewegt, so bewegt sich die Schicht direkt an der bewegten Platte mit derselben Geschwindigkeit mit, da die Teilchen an der Platte haften.
Dabei gleiten die weiter innen liegenden Schichten mit unterschiedlichen Geschwindigkeiten abnehmend in Richtung der ruhenden Platte aneinander vorbei. Die Geschwindigkeit nimmt im einfachsten Fall von der bewegten Platte bis zur ruhenden Platte linear ab. Um überhaupt die Platte in Bewegung zu versetzen ist eine Beschleunigungskraft F erforderlich, die der Widerstandskraft Fw entspricht. Nach Newton ist die Beschleunigungskraft F proportional dem Geschwindigkeitsgefälle dV/dY und proportional der Plattenfläche A.
Hieraus abgeleitet ergibt sich die folgende Gleichung, die bereits einen Proportionalitätsfaktor enthält:
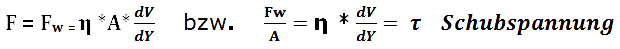
Der Proportionalitätsfaktor η gilt als Maß für die absolute Zähigkeit des Fluids.
η ist somit ein Zähigkeitsmaß welches dynamische Viskosität oder in Kurzform Viskosität genannt wird.
Die Viskosität ist eine typische Stoffeigenschaft, die sowohl Flüssigkeiten als auch Gase betrifft.
Da die Viskosität auf der inneren Reibung beruht, beeinflusst die Temperatur des Fluids die Viskosität in erheblichem Maße. Hieraus ergibt sich zwangsläufig, dass die Viskosität immer mit der zugehörigen Temperatur genannt werden muss.
Flüssigkeiten und Gase verhalten sich im Bezug auf die Viskosität mit steigender Temperatur genau umgekehrt. Während bei Flüssigkeiten mit steigender Temperatur die Viskosität abnimmt, steigt sie bei Gasen.
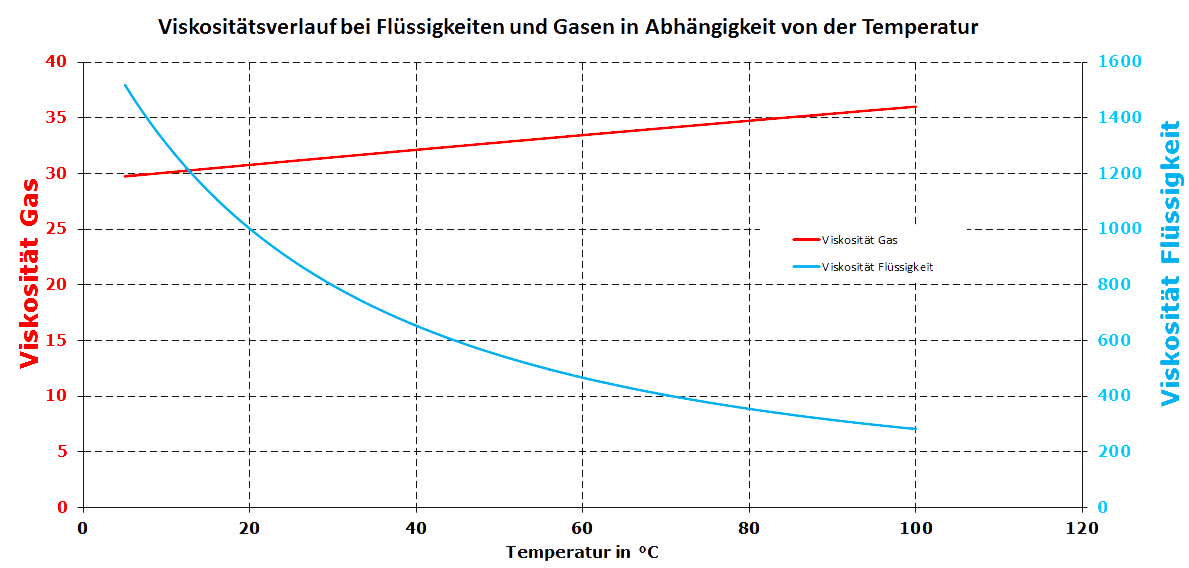
Neben der Temperaturabhängigkeit wir die Viskosität bei Gasen auch durch deren Druck bestimmt. Oberhalb eines Druckes von 20 bar ist die Beeinflussung der Viskosität deutlich. Jedoch ist der Einfluss des Druckes deutlich geringer als der Einfluss der Temperatur. Die Temperaturabhängigkeit der Viskosität lässt sich mit Hilfe der Sutherland-Gleichung beschreiben. Es gilt:
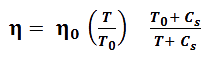
| η | Pa s | Dynamische Viskosität bei der Temperatur |
| η0 | Pa s | Referenz-Viskosität bei der Referenz-Temperatur T0 |
| T | K | Temperatur |
| T0 | K | Referenztemperatur |
| Cs | K | Sutherlands Konstante |
In der unten dargestellten Tabelle finden Sie einige Werte für Sutherland-Konstanten für verschiedene Gase. Die Konstanten gelten aber nur in einem bestimmten Temperaturbereich als hinreichend genau. Der Bereich ist abhängig vom Gas, und der als zulässig erachteten Abweichung gegenüber der tatsächlichen Viskosität.
In der Tabelle finden Sie Werte die der Literatur entstammen und von uns ermittelte Werte. Auch in der Literatur werden teilweise unterschiedliche Werte genannt, je nach den Bereichsgrenzen. Sie finden weiterhin einen Hinweis auf die maximale absolute Abweichung in dem betrachteten Bereich (0°C - 100°C und 0°C bis 300°C).
Letztlich können Sie mit Kenntnis der tatsächlichen Viskositäten z.B. mit Hilfe von Excel VBA recht einfach eigene Konstanten definieren, die Ihren Erwartungen entsprechen. Selbstverständlich kann man so auch für verschiedene Bereiche eigene Konstanten definieren.
| Gas | η [Pa* s] |
T0 [K] |
Cs [K] |
[1] | [2] |
| Luft | 17,16 | 273,15 | 110,4 | Nicht überprüft | Nicht überprüft |
| Wasserstoff | 8,3969 | 273,15 | 84,4 | 0,85% | 0,85% |
| Wasserstoff * | 8,3969 | 273,15 | 80,76 | 0,62% | 0,62% |
| Kohlendioxid | 13,818 | 273,15 | 222,2 | 3,15% | 1% |
| Kohlendioxid * | 13,818 | 273,15 | 262,45 | 0,3% | 0,26% |
| Sauerstoff | 19,055 | 273,15 | 138,9 | 0,28% | 0,28% |
| Sauerstoff * | 19,055 | 273,15 | 137,91 | 0,24% | 0,23% |
| Stickstoff | 16,637 | 273,15 | 106,7 | 1,53% | 0,39% |
| Stickstoff * | 16,637 | 273,15 | 118,01 | 0,23% | 0,23% |
| Helium | 18,694 | 273,15 | 79,6 | 1,58% | 0,44% |
| Helium * | 18,694 | 273,15 | 85,6 | 0,82% | 0,81% |
| Argon | 20,956 | 273,15 | 148 | 0,2% | 1,17% |
| Argon * | 20,956 | 273,15 | 157,68 | 0,24% | 0,24% |
| Neon | 29,385 | 273,15 | 64,1 | 0,62% | 0,51% |
| Neon * | 29,385 | 273,15 | 64,64 | 0,55% | 0,55% |
| * Werte für die Sutherland-Konstante wurden für den Bereich 0°C-300°C über Excel VBA ermittelt. Alle anderen Sutherland-Konstanten sind Literaturwerte. |
|||||
[1] Größte Abweichung im Bereich 0°C bis 300°C
[2] Größte Abweichung im Bereich 0°C bis 100°C
Die Tabelle unterhalb zeigt den Einfluss verschiedener Sutherland-Konstanten bei unterschiedlichen Temperaturbereichen für Sauerstoff und Stickstoff (Druck= 1,01325 bar). Es ist deutlich zu erkennen, dass speziell für einen sehr tiefen Temperaturbereich die aus der Literatur bekannten Sutherland Konstanten nur hinreichend genaue Ergebnisse liefern. Achten Sie beim Gebrauch der Sutherlandgleichung und deren Konstanten also unbedingt auf die Grenzbereiche oder definieren Sie eigene Konstanten. Bei der Definition eigener Konstanten müssen natürlich die Referenzwerte der Viskositäten bekannt sein.
| Gas | η0 [Pa*s] |
T0 [K] |
Cs [K] |
Größte Abweichung -100°C bis 300°C |
| Sauerstoff | 12,904 | 173,15 | 138,9 | 1,9% |
| Sauerstoff | 12,904 | 173,15 | 137,91 | 1,78% |
| Sauerstoff | 12,904 | 173,15 | 127,32 | 0,67% |
| Gas | η0 [Pa*s] | T0 [K] |
Cs [K] |
Größte Abweichung -170°C bis 0°C |
| Sauerstoff | 7,9832 | 103,15 | 138,9 | 6,04% |
| Sauerstoff | 7,9832 | 103,15 | 137,91 | 5,86% |
| Sauerstoff | 7,9832 | 103,15 | 127,32 | 3,89% |
| Sauerstoff | 7,9832 | 173,15 | 104,53 | 0,74% |
| Gas | η0 [Pa*s] |
T0 [K] |
Cs [K] |
Größte Abweichung -100°C bis 300°C |
| Stickstoff | 11,438 | 173,15 | 106,7 | 1,15% |
| Stickstoff | 11,438 | 173,15 | 118,01 | 1,63% |
| Stickstoff | 11,438 | 173,15 | 109,03 | 0,61% |
| Gas | η0 [Pa*s] |
T0 [K] |
Cs [K] |
Größte Abweichung -170°C bis 0°C |
| Stickstoff | 7,1722 | 103,15 | 106,7 | 2,66% |
| Stickstoff | 7,1722 | 103,15 | 118,01 | 5,03% |
| Stickstoff | 7,1722 | 103,15 | 109,03 | 3,14% |
| Stickstoff | 7,1722 | 103,15 | 92,74 | 0,54% |
Im Diagramm unterhalb sind die dynamischen Viskositäten für verschiedene Gas bei 1 bar für unterschiedliche Temperaturen dargestellt.
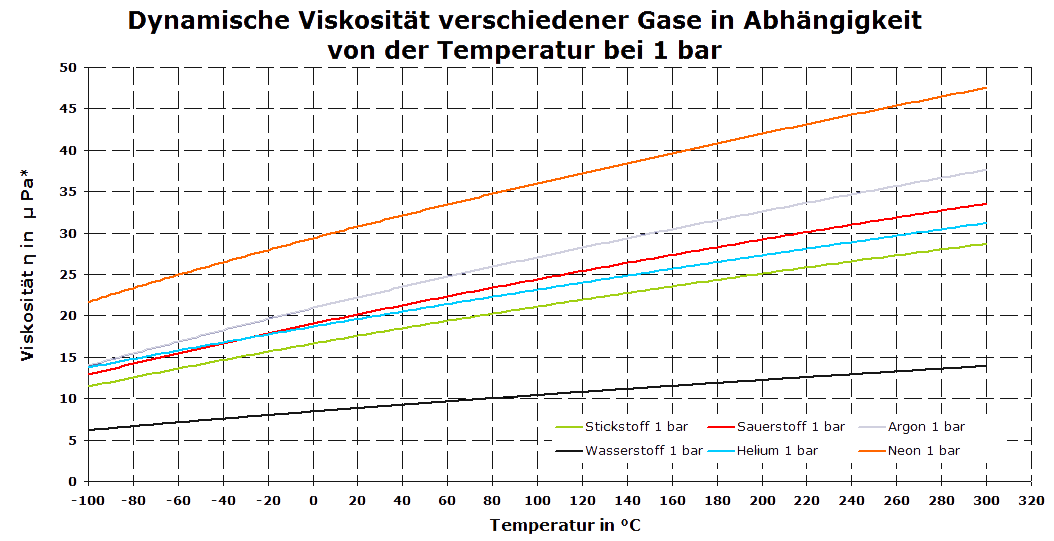
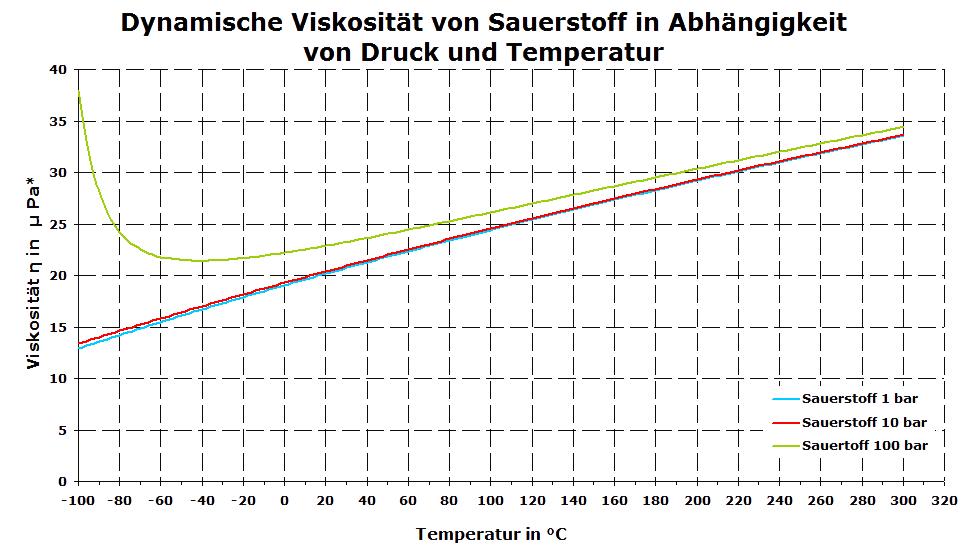
Im anschließenden Diagramm ist exemplarisch für Sauerstoff die Abhängigkeit der Viskosität vom Druck bei unterschiedlichen Temperaturen dargestellt.
Oberhalb von 20 bar sollte die Druckabhängigkeit der Viskosität für Gase berücksichtigt werden.
Für unpolare Gase findet sich in der Literatur eine empirische Methode nach Jossi, Stiel und Thodos.
Neben der dynamischen Viskosität wird in der Strömungstechnik auch häufig mit der kinematischen Viskosität gerechnet. Die kinematische Viskosität ist definiert als das Verhältnis der dynamischen Viskosität/Dichte.
Kinematische Viskosität:
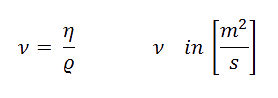
In der unten dargestellten Tabelle finden Sie die dynamische- und kinematische Viskosität von Stickstoff bei 1,01325 bar für verschiedene Temperaturen.
| Kinematische Viskosität von Stickstoff bei 1,01325 bar | |||
| Temperatur in [°C] |
Dichte in [Kg/m]3 |
Dynamische Viskosität 10-6 [Pa*s] |
Kinematische Viskosität 10-7 [m2/s] |
| -150 | 2,802 | 8,4554 | 30,1752 |
| -100 | 1,979 | 11,4390 | 57,8048 |
| -50 | 1,532 | 14,1480 | 92,3499 |
| 0 | 1,250 | 16,6370 | 133,0534 |
| 50 | 1,057 | 18,9470 | 179,3374 |
| 100 | 0,915 | 21,1080 | 230,7667 |
| 200 | 0,721 | 25,0780 | 347,7067 |
| 300 | 0,595 | 28,6840 | 481,7763 |
| 500 | 0,441 | 35,1270 | 795,8629 |
Tabellarische Werte für Viskositäten bei unterschiedlichen Drücken für verschiedene Gase finden Sie nachfolgend.
Eine Übersicht über Online Tools rund um Gase finden Sie unter Online Tools